February 9, 2023

The Mitsubishi Chemical Group（Mitsubishi Chemical）, Keio University (headquartered in Minato, Tokyo, President Kohei Itoh) and IBM Japan, Ltd. (headquartered in Chuo, Tokyo, General Manager Akio Yamaguchi), are pleased to announce that a paper describing the research results of “a new computational method for energy calculations of photonic materials on quantum computers,” a joint project from IBM Quantum Network Hub at Keio University, has been published in “npj Computational Materials,” a world-renowned Nature Research Journal.

Mitsubishi Chemical, Keio University and IBM Japan developed [A] a spin-restricted quantum ansatz, [B] a new excited states calculation method called the variational quantum eigensolver under automatically-adjusted constraints (VQE/AC method) to accurately calculate energies of photonic materials on quantum computers. By applying both [A] and [B] to the quantum chemistry calculations for the molecular structures related to light absorption and non-radiative decay of phenol blue dye on IBM Quantum System One, which is the first gate-based quantum computer installed in Japan, the ground state and excited state energies could be successfully computed that are within 2 kcal/mol of exact values.

This research is expected to pave the way for geometry optimization calculations of the ground and excited states, which is indispensable for the understanding and design of photonic materials.

Key research findings

・Spin-restricted quantum ansatz and VQE/AC method¹ was developed for quantum chemistry calculations of photonic materials on quantum computers.
・By using the spin-restricted quantum ansatz, the error of energy calculations is minimized.
・Using the VQE/AC method eliminates the need for pre-determination of parameters in conventional methods.
・The developed methods are expected to be applied to the calculation of geometry optimizations, which is indispensable for the understanding and design of photonic materials.

Background

For a deep understanding of chemical mechanism and rational molecular design of photonic materials, it is necessary to accurately predict properties such as the wavelengths and intensities of light absorption and emission, and the ratio of non-radiative decay which are not associated with emission of light. To predict these properties, it is essential to quantitatively calculate the energies of the ground state² and excited state³ for the molecular geometries (FC geormetry⁴ and CI geormetry⁵) where each phenomenon is most likely to occur. Currently, the TDDFT method⁶ is most widely used to calculate excited states, but it is known that when the energies of the ground and excited states are degenerate or nearly degenerate, as in CI structures, the TDDFT method cannot correctly calculate the energy, and a multireference calculation method⁷ must be used instead. However, applying multireference calculations to complicated molecular systems is prohibitively computationally expensive.

Quantum computing is attracting attention as a computation method for effectively solving this problem. In order to calculate excited states on a quantum computer, a quantum ansatz⁸ capable of representing the ground and excited states and an appropriate cost function for the excited state calculation must be used. Because calculations on a current quantum computer always have errors⁹, designing a quantum ansatz that minimizes errors has been an important task. In addition, since the appropriate cost function for excited state calculations differs from one molecular geometry to another, a calculation method that can be applied commonly to all molecular geometries is needed.

Achievements of this research project

In this study, we have succeeded in calculating excited states with smaller errors than conventional method by using [A] a developed quantum ansatz that can restrict the spin multiplicity of the trial wavefunction (spin-restricted ansatz) and [B] a developed method for calculating excited states without using cost function (VQE/AC method)

[A] spin-restricted ansatz

In constructing a quantum ansatz, we imposed the condition that the spin multiplicity of the ground and excited states be restricted. For example, a singlet state containing two electrons in two molecular orbitals (HOMO and LUMO¹⁰) is represented by the superposition of three electron configurations shown in Figure 2a. By using a quantum ansatz (Fig. 2b) that only represents these three electron configurations, we can avoid wrong electron numbers and different spin multiplicities, which is one of the causes of errors. In fact, we have shown that energy calculations with spin-restricted ansatz can provide smaller errors than other common quantum ansatz circuits.

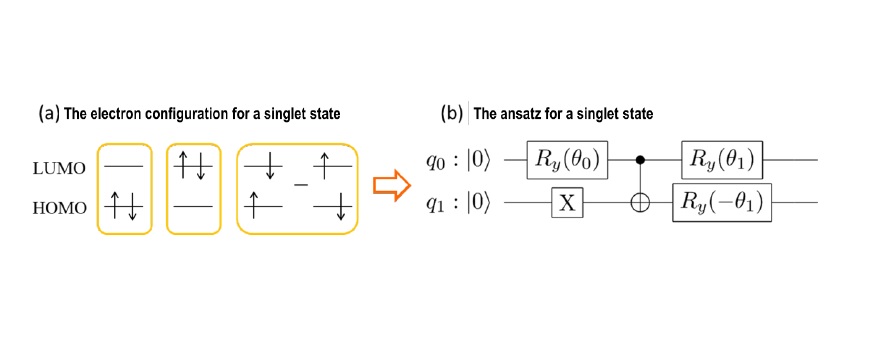
Fig 2. Construction of the spin-restricted ansatz

(a) The electron configuration for a singlet state including 2 electrons in two orbitals (HOMO and LUMO). (b) The ansatz representing the superposition of three electron configurations of the singlet state. Two solid lines of q0 and q1 depict two qubits. The energy is obtained by optimizing parameters of q0 and q1 contained in the qubit operations represented by the squares with classical computers.

[B] The method (VQE/AC) for calculating excited states without using cost function

In the conventional excited state calculation (VQD method¹⁰), the energy is obtained from minimizing the cost function, as shown in Figure 3, in which the parameters b and g are predetermined. It was difficult to reliably describe the potential energy surface¹¹ using the VQD method because the appropriate values for the predetermined parameters b and g, depend on the molecular geometries. The value of g can be fixed to zero by using the spin-restricted ansatz. Moreover, the tunning of b can also be avoided by using a constrained optimization method in the presence of |⟨𝛹𝛹(𝛉𝛉)|𝛹𝛹0⟩|2 being close to zero. We named this method excited state calculation VQE under automatically-adjusted constraints (VQE/AC method) of which the constraint in the optimization process is satisfied for the excited state.

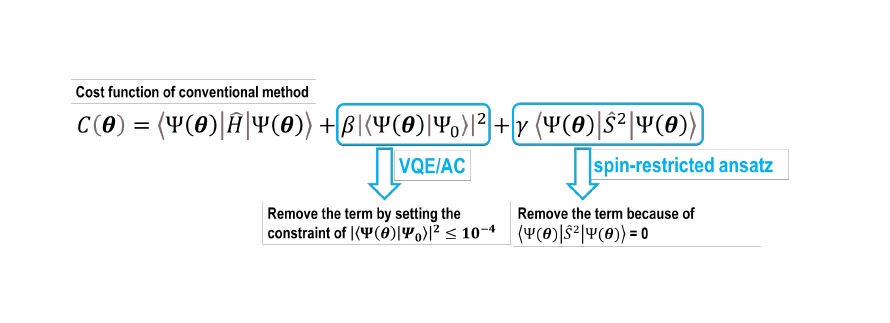
Fig 3. The Cost function, 𝐶𝐶(𝛉𝛉), of conventional method and the description of the concept of the VQE/AC method

The combination of the spin-restricted ansatz and the VQE/AC method was applied to the ground and excited states calculations of phenol bule dye with CASSCF¹³ method, a type of multi-reference calculation method, on IBM Quantum System One which is a gate-based quantum
computer installed at the Kawasaki Business Incubation Center in Shin Kawasaki Sozo no Mori. Consequently, we successfully obtained a small error from the calculations for both the FC and CI geometries that are within only 2 kcal/mol of exact values.

Future works

Although the VQE/AC method was developed for excited state calculations, it can be applied to the calculation of various states, not only excited states, by changing the constraints. Since by using the VQE/AC method the ground and excited state energies could be computed with the same calculation condition for any molecular geometry, in the future we expect to apply the method to optimize different geometries such as the most stable geometry and the crossing point between the electronic states.

The published paper: https://doi.org/10.1038/s41524-023-00965-1

Glossary

¹ VQE/AC method:
Abbreviation of calculation method of variational quantum eigensolver under automatically-adjusted constraints developed in this study.

² Ground state:
The stationary state of the lowest energy.

³ Excited state:
Any state with energy greater than the ground state. A molecule can be promoted to the excited state by absorbing light which has the energy being equal to the difference between the ground and excited states.

⁴ FC geometry:
Abbreviation of the Frank-Condon geometry. It is the most stable geometry of the ground state and is also the geometry for which the light absorption is most likely to occur.

⁵ CI geometry:
Abbreviation of the Conical intersection geometry. The energies of the ground and excited state of the geometry are degenerate. Decay from excited state is most likely to occur through the geometry.

⁶ TDDFT method:
Abbreviation of Time-dependent density functional theory.

⁷ Multireference calculation method:
A method consists of multi electron configurations as references to describe ground and excited states. There are many classes of multireference calculation method, including the multireference configuration interaction method (MRCI), multireference perturbation theory (MRPT), and the multireference self-consistent field method (MRSCF).

⁸ Quantum ansatz:
A sequence of quantum gates for operating qubits and the measurements of qubits state.

⁹ Error:
Statistical errors and errors originating from noise of the quantum computer are collectively described as error.

¹⁰ HOMO and LUMO:
HOMO is the most unstable occupied molecular orbital and LUMO is the most stable unoccupied molecular orbital.

^VQD method:
Abbreviation of variational quantum deflation.

¹² Potential energy surface:
A plot of energy as a function of geometry coordinates.

¹³ CASSCF:
Abbreviation of complete active space self-consistent field. CASSCF is an approach of MRSCF in which both the set of weights and molecular orbitals of the electron configurations are optimized to obtain the lowest energy.

Co-authors
・Shigeki Gocho, Miho Hatanaka and Taichi Inagaki, Keio University
・Qi Gao, Takao Kobayashi and Shu Kanno, Mitsubishi Chemical Group Corporation
・Hajime Nakamura, IBM Research-Tokyo