22 January 2016

by Hayley Dunning

Physicists from Imperial and Germany have demonstrated a theory about the behaviour of light in materials, 106 years after it was first proposed.

Normally, light waves slow down when they reach the boundary between a material and air, so that a beam of light is bent in a different direction. A classic example of this simple refraction is a spoon appearing bent in a glass of water.

However, a more complicated, and quite peculiar type of refraction is seen in some materials such as crystals, when light waves hit the boundary at special angles. The light beam does not stay together, but rather splits into a cone shape, appearing as a hollow cylinder as it exits the material.

This conical refraction was first proposed by William Hamilton in 1832, and was a crucial prediction of Fresnel’s theory about the wave nature of light. It was proven shortly thereafter in natural crystals such as the mineral aragonite. In these materials, there are two directions light can go in to produce the conical effect, producing four ‘double points’ of crossover.

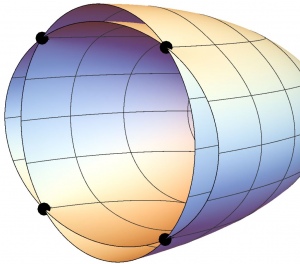
Simple conical refraction with 4 double points

While conical refraction was proven, its limits were still to be explored. In 1864, the mathematician Ernst Kummer proposed a surface that has 16 double points, and in 1910 mathematician Harry Bateman suggested this surface could describe the behaviour of light in some materials, and that conical refraction could happen in 16 different directions.

At the time, no natural material existed that could test this idea. But with the rise of metamaterials – which can be engineered to have properties that are not found in nature – the theory could finally be put to the test.

Now, by creating a computer model of a metamaterial with just the right properties, Dr Alberto Favaro from Imperial College London’s Department of Physics along with Prof Friedrich Hehl from the University of Cologne, Germany, have shown that conical refraction can be produced in more directions. In fact, testing their model to the limit, they show that 16 double points is the maximum allowed, as in Kummer’s theory.

Proving greatness

“I often wonder if Bateman imagined that his ideas on light and Kummer surfaces would prove their greatness 106 years after publication. Working on a topic that has such an interesting history was, for us, a real pleasure.”

“It’s exciting to be able to investigate a theory that links mathematics and physics in this way, and it opens the door to verifying lots of other possible links,” Dr Favaro added. “There are all sorts of wonderful surfaces in mathematics that physicists can take and say ‘what are the corresponding materials, and what unexpected properties will they have?’”

“With metamaterials, we can now engineer materials in a more powerful way so that we are no longer constrained by what nature gives us,” he said.

In the study, published today in the journal Physical Review A, Dr Favaro and Prof Hehl propose building blocks for the metamaterial that could physically test the phenomenon, and others like it. The team hope experimental physicists will take on the challenge and create the material. 

'Light propagation in local and linear media:Fresnel-Kummer wave surfaces with 16 singular points' By A Favaro and F Hehl is published in Physical Review A.