16th December, 2015

Researchers at Nippon Telegraph and Telephone Corporation (NTT; Head office: Chiyoda-ku, Tokyo, Japan; President and CEO: Hiroo Unoura) have proposed an ‘all-photonic intercity quantum key distribution (QKD)’ protocol that doubles the achievable distance of ultimately secure quantum cryptography^*1 without decreasing the efficiency, using only optical devices without quantum repeaters^*2. This protocol enables us to expand the communication range from 400 km to 800 km (Fig. 1), rendering quantum cryptography between major cities realizable before the arrival of (currently challenging) quantum repeaters.

From its high security, quantum cryptography holds promise for performing such confidential communication over a network as to be required for a plebiscite, a top-level meeting, a financial deal, an exchange of genetic/biological information and so on. Intracity quantum cryptography based on conventional schemes has already been ready for practical use. But, to expand the communication range against photon loss in optical fibres, quantum repeaters were needed. Still, quantum repeaters are certainly necessary for intercontinental communication, but they may be too demanding to be used to connect metropolis within a 1,000 km radius, owing to their need of a challenging technique such as ‘matter quantum memories’^*3 and ‘quantum error correction’^*4. In contrast, our scheme works, using only a single intermediate node with optical devices alone without the challenging techniques. Nonetheless, our scheme could outperform even quantum repeaters for communication distances below 800 km. The point of our discovery is to derive latent ‘adaptiveness to photon loss’ from a ‘time-reversed’ QKD protocol.

This work is made public by the journal Nature Communications on 16th December in 2015.

This research is in part executed under the Project UQCC by the National Institute of Information and Communications Technology (NICT).

Due to recent rising of various security incidents, interests in security are increased more than before. Communication is not an exception, and, for instance, the National Security Agency (NSA) of the USA announces preliminary plans for transitioning to quantum resistant cryptographic algorithms from the current ones (like RSA^*5) crackable by a quantum computer [NSA’s press release on 19th August in 2015: https://www.nsa.gov/ia/programs/suiteb_cryptography/]. There are several candidates (including mathematical ones) for cryptography so robust to be resistant to quantum computers. But, so far, quantum cryptography— which is secured by the law of physics—has been the only protocol that is proven to be secure even against quantum computers. Quantum cryptography with such ultimately high security is expected to enable us to perform such confidential important communication over a network as to be required for a plebiscite, a top-level meeting, a financial deal, an exchange of genetic/biological information and so on.

Quantum cryptography is based on the transmission of photons^*6 over optical fibres. In fact, based on the direct transmission of photons between a sender and a receiver, conventional QKD schemes have already been commercially available for 100-km communication distances and, in Japan, ‘Tokyo QKD network’^*7 has been running as the testbed since 2010. Therefore, with the conventional schemes, intracity QKD links (over about 100 km) are available even at present. However, owing to the photon loss in the optical fibre (which increases exponentially with the length), about 400 km are considered to be the maximum distance of the conventional schemes. Thus, to connect QKD networks in different cities above 400 km distant, we needed ‘quantum repeaters’, rather than the conventional schemes based on the direct transmission. Since quantum repeaters enable us to perform QKD over any communication distance efficiently (only with polynomial resources with the distance), proof-of-principle experiments for quantum repeaters have extensively been performed by lots of research groups in the world. However, quantum repeaters necessitate many intermediate nodes connected with optical fibres, each of which needs a very challenging technique such as matter quantum memories and quantum error correction. These requisites are necessary to achieve an extremely high goal such as intercontinental QKD connections. But, they may be too demanding to connect different major cities about 1,000 km distant.

Researchers at NTT have proposed a new scheme—called ‘all-photonic intercity QKD’—which doubles the communication distance of the QKD without decreasing its efficiency. Nonetheless, this scheme uses only a single intermediate node equipped with optical devices alone, without matter quantum memories and quantum error correction required in quantum repeaters (Figs. 2 and 3 and Table 1). This scheme could outperform quantum repeaters (based on atomic ensembles) for communication distances below 800 km, and it expands the communication range—which is 400 km for conventional schemes—to 800 km (Fig. 1). In addition, since the proposed scheme does not use matter quantum memories similarly to all-photonic quantum repeaters^*8 [NTT’s press release on 15th April in 2015: http://www.ntt.co.jp/news2015/1504e/150415a.html], (a) it displays the communication speed in the same order of the repetition rate of optical devices, irrespective of the communication distance, (b) it does not need a still challenging interface between matter and photons and (c) it could work at room temperature in principle. Therefore, our scheme could work as cost-effective backbone links to connect metropolises within a radius of 800 km. The point of our discovery is to find out latent ‘adaptiveness to photon loss’ that is held only by the ‘time-reversed’ QKD protocol among many existing QKD schemes.

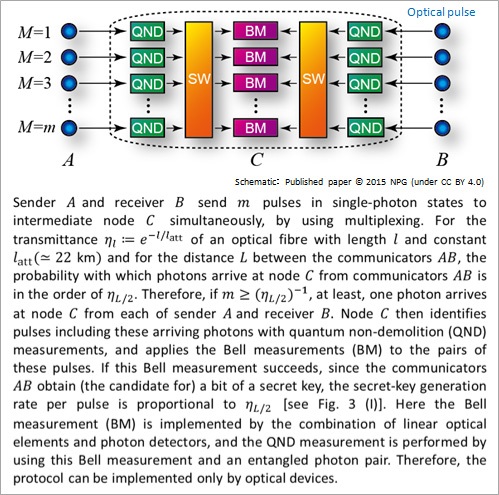
Figure 2: All-photonic intercity QKD

Our all-photonic intercity QKD protocol bridges a large technological gap between intracity QKD links with conventional schemes and the future intercontinental QKD links with quantum repeaters, assigned a new role to connect metropolises. Therefore, if optical devices required in our protocol—linear optical elements^*9, single-photon sources^*10, photon detectors^*11 and active feedforward techniques^*12—are developed further, ultimately secure cryptographic communication between domestic hubs within a 800 km radius or neighbouring capitals will be presented in the near future. Not only does this expand the market of quantum cryptography, but this will also realize the ultimately secure communication network for our social life. If our scheme is combined with the all-photonic quantum repeater protocol—which is implementable only with the same optical devices—for intercontinental links, it is made seamless to realize the high-speed and cost-effective ‘all-photonic’ QKD network based only on optical devices on a global scale. Therefore, subsequently to the practical use of the conventional QKD schemes, the research and development of optical devices contribute to realize all-photonic intercity QKD, all-photonic quantum repeaters and an all-photonic quantum computer^*13 in order, opening up the future of the ‘quantum’ information society. Towards the creation of such a quantum information society, NTT continues to develop our strength in the research and development for the cutting-edge optical devices.

The goal of a QKD scheme is to supply a ‘secret key’—which is a resource for unconditionally secure communication—to a sender and a receiver, and its performance is thus estimated in terms of the secret-key generation rate^*1. It has recently been proven [NICT’s press release on 24th October in 2014: http://www.nict.go.jp/en/press/2014/10/29-1.html] that the secret-key generation rates of the simplest QKD schemes based on the direct transmission of photons must decrease linearly with the transmittance of the optical fibre between the communicators [Fig. 3 (Ⅳ)], irrespectively of the details of the schemes. Therefore, we cannot hope that they have big improvement in the performance. Hence, we focus on the second-simplest schemes, which use an intermediate node in the middle of the communicators.

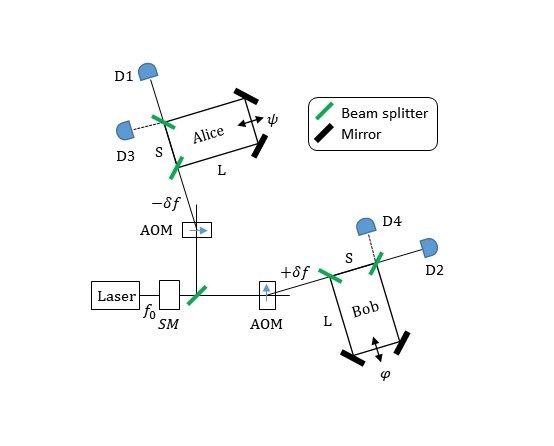
The conventional schemes utilizing the intermediate node are an entanglement-based protocol and its time-reversed version (Fig. 4). In the entanglement-based protocol (Fig. 4a), the intermediate node prepares a photon pair in an entangled state^*14, and then distributes halves of the pair to the sender and the receiver through optical fibres, respectively. The requisite for the success is that both of these photons arrive at the sender and the receiver. Since the success probability here is proportional to the transmittance of a fibre between the communicators, the secret-key generation rate is similar to the direct-transmission schemes’. Even as for the time-reversed protocol (Fig. 4b), since this is merely a simple time reversal of the entanglement-based scheme, the secret-key generation rate is also proportional to the transmittance of a fibre between the communicators [Fig. 3 (Ⅲ)], which is similar to the direct-transmission schemes. However, these protocols are different in room for improvement. In particular, in the entanglement-based protocol, since the pairing of the entangled photons is determined before the fibre transmission, the protocol cannot be changed so as to depend on the occurrence of the photon loss in the optical fibres. On the other hand, in the time-reversed protocol, pairing for the ‘Bell measurement’ to supply entanglement for photons can be determined after the fibre transmission. This is the room for improvement held only by the time-reversed protocol. Our all-photonic intercity QKD exactly utilizes this room.

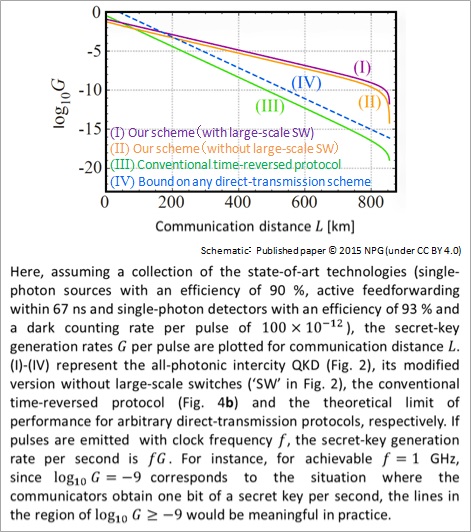
Figure 3: Performance comparison

More precisely, in the all-photonic intercity QKD protocol (Fig. 2), the sender and the receiver send photons to the intermediate simultaneously, by using multiplexing. Then, the intermediate node finds photons that successfully arrive there. Among them, the intermediate node makes photons from Alice be paired with ones from Bob, and then applies the Bell measurements to the pairs. If the Bell measurement succeeds, the protocol presents (the candidates for) a secret key to the sender and the receiver. Therefore, in the all-photonic intercity QKD protocol, the intermediate node chooses the pairing of photons to be entangled, depending on the occurrence of the photon loss in the fibre transmission, which is the difference from the entanglement-based protocol and the time-reversed protocol. In fact, thanks to this difference, the secret-key generation rate (per pulse) of the all-photonic intercity QKD protocol is in the order of the transmittance of a fibre not between the communicators but between the sender (or the receiver) and the intermediate node [Fig. 3 (Ⅰ)]. Hence, the all-photonic intercity QKD protocol doubles the communication distance with retaining the same secret-key generation rate as the conventional schemes’. In addition, in the paper, we present a modified protocol that uses single-mode on/off switches, a static linear optical circuit and photon detectors, instead of the large-scale optical switch and the Bell measurements required in the original protocol (Fig. 2), whose performance is given in Fig. 3 (Ⅱ).

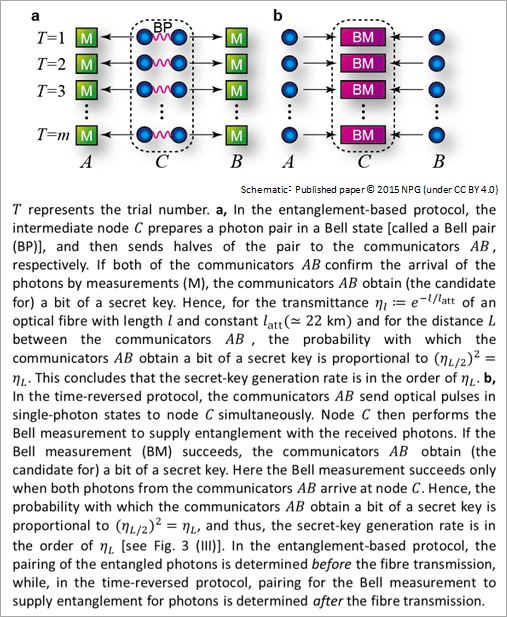
Figure 4: Conventional schemes with an intermediate node

If we calculate the performance of the all-photonic intercity QKD by assuming a collection of the state-of-art technologies (Fig. 3), we notice the followings: (1) Our protocol outperforms the conventional time-reversed protocol [Figs. 4b and 3 (Ⅲ)] for the communication distances larger than 100 km. (2) Our protocol outperforms the theoretical limit of the performance of arbitrary protocols based on the direct transmission of photons [Fig. 3 (Ⅳ), NICT’s press release on 24th October in 2014: http://www.nict.go.jp/en/press/2014/10/29-1.html]. (3) The performance of our protocol is seven orders of magnitude better than that of the conventional time-reversed protocol for the communication distance of 800 km [Fig. 3 (Ⅰ)-(Ⅲ)]. (4) Our protocol outperforms even quantum repeaters based on atomic ensembles [N. Sangouard et al., Rev. Mod. Phys. 83, 33 (2011)] for the communication distances less than 800 km, if it works with a clock frequency of 100 MHz.

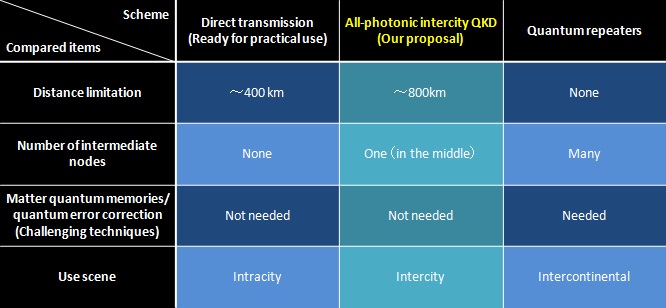
Table 1: Position of all-photonic intercity QKD

Publication information

Koji Azuma, Kiyoshi Tamaki and William J. Munro,
‘All-photonic intercity quantum key distribution’,
Nature Communications [16th December, 2015 (BST)].
doi: 10.1038/ncomms10171

Glossary

^*1 Quantum cryptography

If a sender and a receiver share a ‘secret key’ that is composed of random bits unpredictable by anyone (except for the sender and the receiver), by consuming it, they can perform cryptographic communication through public communication channels such as the wireless communications and the Internet (Vernam cipher). Quantum cryptography is a method to supply the sender and the receiver with such a secret key through the exchange of quantum superposition states between them. It is also called ‘quantum key distribution (QKD)’. For instance, in QKD over a hundred kilometres, the sender and the receiver generate bit strings via exchanging photons^*6 between them, correct the bit errors in the bit strings and then properly shorten the reconciled bit strings according to the estimation of the leaked information to the eavesdropper (nature) in order to obtain a secret key.

^*2 Quantum repeaters

The goal of quantum repeaters is to supply quantum entanglement^*14—which is a resource for any quantum communication—to the sender and the receiver efficiently (with the polynomial resources with the communication distance), by utilizing repeater nodes between them. The method is mainly composed of the ‘entanglement generation process’ and the ‘entanglement swapping process’. Quantum repeaters are needed to perform long-distance quantum communication.

^*3 Matter quantum memory

Quantum memory is the function to store the quantum superposition states for a certain period of time. For instance, in contrast to the memory in the conventional computers that can store both of bit values 0 and 1, quantum memory can keep not only 0 and 1 but also their quantum superposition states.
A ‘matter quantum memory’ is the realization of the quantum memories based on matter such as an atomic ensemble, a single atom, an ion trap, a quantum dot, a superconducting qubit and a nitrogen-vacancy centre in a diamond.

^*4 Quantum error correction

Encoding a (logical) qubit into plural physical qubits to make it resilient against the effect of noise.

^*5 RSA cryptography

Public-key cryptosystem whose security is based on the practical difficulty of factoring large integers. This name is due to the initials of the inventors, R. Rivest, A. Shamir and L. Adleman. Since the prime factorization of large integers is solvable by a quantum computer efficiently, RSA cryptography, including all the past date that have been exchanged based on it, is cracked once a quantum computer is realized.

^*6 Photon

The particle-like aspect of light. A single photon is the unit of energy of light that cannot be divided further. For instance, if we input a single photon into a beam splitter, the output photon is in a quantum superposition state.

^*7 Tokyo QKD network [http://www.nict.go.jp/en/press/2010/10/14-1.html]

QKD network using part of NICT’s open fibre test-bed network JGN2plus, operated by the NICT in cooperation with its commissioned research partners NEC, Mitsubishi Electric and NTT. In this field network operation, Toshiba Research Europe Ltd and other European organizations have also participated in an effort to promote standardization of the interconnection technology between Japanese and overseas QKD systems.

^*8 All-photonic quantum repeaters [http://www.ntt.co.jp/news2015/1504e/150415a.html]

Quantum repeater protocol that is implementable by using only optical devices such as linear optical elements^*9, single-photon sources^*10, photon detectors^*11 and active feedforward techniques^*12, in contrast to conventional quantum repeater schemes that necessitate not only optical devices but also matter quantum memories.

^*9 Linear optical elements

Passive optical devices preserving the number of photons. The examples are a beam splitter, a half-wave plate, a quarter-wave plate, a phase shifter and a polarizing beam splitter.

^*10 Single-photon source

A source that can output a single photon in an on-demanding manner.

^*11 Photon detector

A detector that can detect a single-photon level of light.

^*12 Active feedforward technique

A technique to switch the linear optical circuit at high speed, depending on the previous measurement outcomes from photon detectors (for instance, by using optical switches).

^*13 All-photonic quantum computer

Quantum computing scheme that is implementable by using only optical devices such as linear optical elements^*9, single-photon sources^*10, photon detectors^*11 and active feedforward techniques^*12. This scheme is also known as the KLM scheme, by taking the initials of the inventors, E. Knill, R. Laflamme and G. J. Milburn.

^*14 Quantum entanglement

A quantum superposition state of composite systems that can never be expressed by any collection of the descriptions of the subsystems. This is an essential resource for quantum communication and quantum computation. The existence has already been experimentally demonstrated by using photons and atoms.