Dec 23, 2014

ANN ARBOR—The most complicated crystal structure ever produced in a computer simulation has been achieved by researchers at the University of Michigan. They say the findings help demonstrate how complexity can emerge from simple rules.

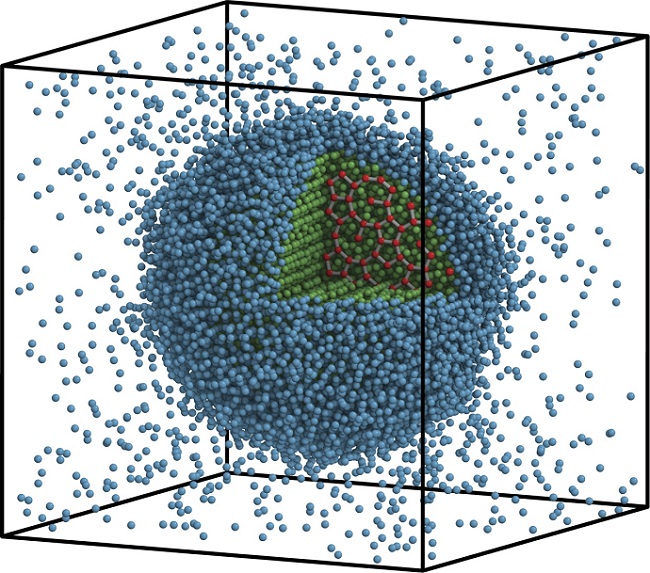
Their "icosahedral quasicrystal" (eye-KO-suh-HE-druhl QUAZ-eye-cris-tahl) looks ordered to the eye, but has no repeating pattern. At the same time, it's symmetric when rotated, like a soccer ball with five-fold and six-fold patches.

This property, called icosahedral symmetry, is frequently found on small scales around a single point. It's in virus shells or buckyballs – molecules of 60 carbon atoms. But it is forbidden in a conventional crystal. Like trying to tile a bathroom floor with pentagons, icosahedra do not nicely fill space, said Michael Engel, a research investigator in the Department of Chemical Engineering and first author of a paper on the findings published in Nature Materials.

"An icosahedral quasicrystal is nature's way of achieving icosahedral symmetry in the bulk. This is only possible by giving up periodicity, which means order by repetition. The result is a highly complicated structure," Engel said.

A cross-section of the icosahedral quasicrystal simulated by University of MIchigan researchers. While the exotic solid has order and rotational symmetry, it does not have a repeating pattern. Image credit: Michael Engel

Icosahedral quasicrystals, commonly found in metal alloys, earned the chemist who discovered them more than 30 years ago a Nobel Prize. But engineers are still searching for efficient ways to make them with other materials. Due to their high symmetry under rotation, they can have a property called a "photonic band gap." A photonic bandgap occurs when the spacing between the particles is similar to that of light. Particles arranged in this way could trap and route light coming from all directions.

"If icosahedral quasicrystals could be made from nano- and micro-meter sized particles, they could be useful in a variety of applications including communication and display technologies, and even camouflage," said Sharon Glotzer, the Stuart W Churchill Collegiate Professor of Chemical Engineering at U-M.

While these applications are tantalizing, they're very much speculation. The researchers say the most exciting aspect of the findings is the insight they provide into how icosahedral quasicrystals form.

"When researchers study quasicrystals in the lab, they typically lack direct information about where the atoms are. They look at how the materials scatter light to figure that out. No one has ever gotten one with icosahedral symmetry to self-assemble thermodynamically in a computer model that's not built by hand, and researchers have been trying for decades," Glotzer said.

Patterns in the quasicrystal simulated by Michigan Engineering researchers reflect the Golden Ratio. The ratio was also found in the relationship of the distances of particle interactions. Image by Michael Engel.

The simulation will allow researchers for the first time to observe how icosahedral symmetry develops.

The U-M simulation was done using only one type of particle, which is unique. Typically, two or even three atomic elements are required to achieve a quasicrystal structure.

Even though the end product showed long-range order, the particles only interacted with those up to three particle-distances away. When the researchers looked closer, they found that the Golden Ratio governed those interactions. The Golden Ratio, which is about 1.61, is a mathematically and artistically important number that was first studied by the ancient Greeks. It's related to the Fibonacci Sequence – the simple progression of numbers beginning with 0 and 1 in which the next number is the sum of the previous two – so 0, 1, 1, 2, 3, 5, 8, 13, etc. It's visible in the arrangement of petals in flowers, seeds in a pinecone, branches in trees and spirals of nautilus shells, for example.

"These findings help answer fundamental questions that are important in all of nature: How do you get really complex arrangements of atoms and molecules from essentially local information? This is a beautiful example of something incredibly rich in structure emerging from very simple rules," Glotzer said.

A paper on the findings titled "Computational self-assembly of a one-component icosahedral quasicrystal" is published online in Nature Materials. Glotzer is also a professor of Materials Science and Engineering, Macromolecular Science & Engineering and Physics in the College of Literature, Science and the Arts. The research was funded by the U.S. Army Research Office, the Department of Defense, and the National Science Foundation.

Related Links:

 - Abstract: Computational self-assembly of a one-component icosahedral quasicrystal:http://www.nature.com/nmat/journal/v14/n1/full/nmat4152.html

 - Interactive visualization of the crystal: http://www.nature.com/nmat/journal/v14/n1/extref/nmat4152-s2.html

 - Sharon Glotzer: http://sitemaker.umich.edu/glotzergroup/home

 - Michael Engel: http://www-personal.umich.edu/~engelmm/