December 4, 2014

Quantum computers will someday perform calculations impossible for conventional digital computers.  But for that to happen, the core quantum information must be preserved against contamination from the environment.  In other words, decoherence of qubits must be forestalled.  Coherence, the ability of a system to retain quantum integrity---meaning that one part of the system can be used to predict the behavior of other parts---is an important consideration.

Over the past dozen years, remarkable experiments have shown how the coherence of a Bose condensate loaded into optical lattices can collapse and later return.  New theoretical work by JQI scientists provides a detailed explanation for this quantum revival.  The heart of their theory are interactions involving three atoms simultaneously.

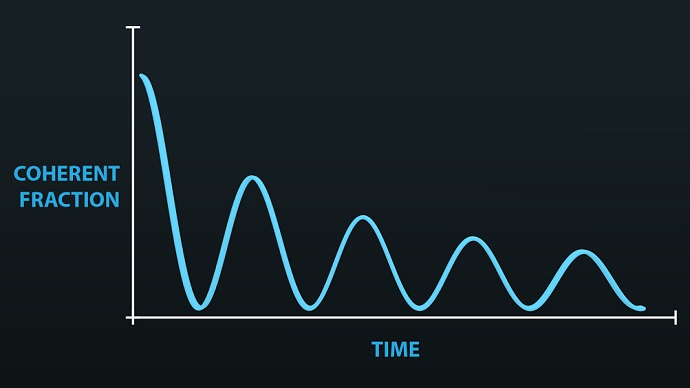
The coherence of the lattice-BEC waxes and wanes with time. Three-atom interactions in the various lattice wells make the overall coherence of the BEC decline and also re-emerge. Credit: JQI/Kelley.

BEC IN AN OPTICAL LATTICE

In Bose Einstein condensates (BECs) typically a million atoms are chilled until their respective waves overlap.  In effect, they become a single coherent object.  If furthermore the BEC is lined up into a series of zones in space using the powerful electric fields of crisscrossing laser beams---a configuration called an optical lattice---then the BEC atoms become a sort of crystal.

The effect of the optical lattice is to encase the atoms in stacks of egg-carton-like confinements. Typically about 100x100x100 (one million) egg-carton slots are filled by a BEC cloud.  For a million-BEC atom BEC this corresponds to about one atom per lattice site. The atoms in this artificial crystal are spaced much farther apart than the atoms in a natural crystal but still close enough for them to interact in interesting ways.

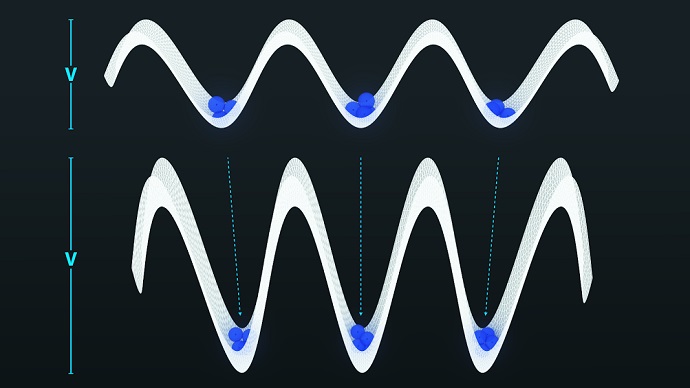
Actually, from a quantum point of view the strength of the BEC’s wave function in each slot or site(which reflects, in turn, the likelihood that the BEC is manifested at that particular point) can be considered as a weighted sum which expresses the likelihood that one atom is present at that spot, plus the likelihood of two atoms, and three atoms, and so forth.  This situation is illustrated in figure 1. 

THE FALL AND RETURN OF COHERENCE

If suddenly the strength of the lasers is increased, the depth of the well becomes deeper, and the atoms are less likely to tunnel from one compartment to another, and consequently more likely to interact with its partners within that well.

What happens to the coherence of the BEC ensemble when atoms are encouraged to interact with each other at close range in the lattice sites?  This is what scientists at the Max Planck Institute for Quantum Physics in Garching, Germany set out to explore in an experiment conducted a dozen years ago.

Trapping rubidium atoms in an optical lattice, and then quickly deepening the potential wells, Immanuel Bloch and his colleagues took images of the BEC after certain intervals.  With no delay at all, the BEC image (recorded by shooting laser light at the BEC atoms after they had been released from all restraint) shows that BEC still retains its full coherence.  That is, the image of the BEC-in-the-lattice looks crystalline.  It appears like x-ray pictures of actual crystals, revealing the fixed positions of the atoms.

But as time goes by the ensemble is less and less like a crystal, meaning that coherence is collapsing.

The story is not over.  If you wait longer, the crystallinity and the coherence comes back.  Atom interactions in the wells undermined coherence but also helped to restore it.  The Max Planck scientists saw coherence (defined as the fraction of atoms that could be found in the principal bright spots in those images of the BECs) come and go over time, but generally damping out to a low number (figure 2).

JQI THEORY

Eite Tiesinga at the Joint Quantum Institute, along with his colleagues Trey Porto and Philip Johnson, stepped up and offered an explanation.  They argued that the crucial ingredient in explaining the coming and going of coherence was three-way interactions in the wells.  They worked out the treatment of forces among three atoms, not just as the sum of all different two-way configurations but also via non-separable interactions of three atoms.  These interactions can be depicted in drawings reminiscent of the Feynman diagrams used in high-energy physics (see figure 3).

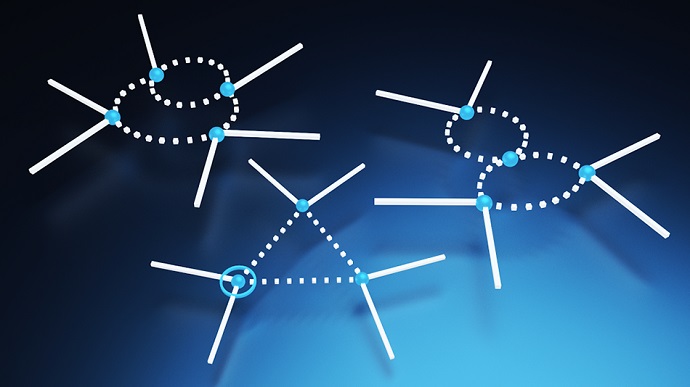
Feynman-like diagrams showing different ways in which three atoms, held inside a potential well, interact all at the same time. Solid lines signify atoms that remain in the lowest energy level of the BEC, while dotted lines signify atoms that temporarily assumed excited energy levels. This seeming non-conservation of energy is allowed under the provision of the Heisenberg uncertainty principle. Credit: JQI/Kelley.

Tiesinga’s theory not only explains the coming and going of coherence seen in the Garching experiment, including the “damping out” of coherence, in terms of true three-atom interactions.  Moreover they predicted the return of a more robust coherence after much longer delay times.  This return was indeed observed in a later experiment.

“In a sense, quantum coherence never really, fully disappears,” says Tiesinga.  “What happens over the short run is what I call ‘de-phasing.’ But the true coherence is still there and will return if you wait long enough.  The revival of coherence is helped along if the temperature of the condensate is closer to absolute zero.”

In a new paper Tiesinga and his co-authors argue that scientists should also study 4-atom and higher-order interactions among atoms in order to get a better understanding of what might be called quantum revivalism or de-phasing or de-decoherence. 

He suggests that using polar molecules, clumps of atoms that have a net electric dipole, would add still more interaction possibilities to this subject.

REFERENCE PUBLICATION
"Universal and nonuniversal effective N-body interactions for ultracold harmonically trapped few-atom systems,"  X.Y. Yin, D. Blume, P.R. Johnson, E. Tiesinga, Phys. Rev. A, 90, 043631 (2014)

"Effective three-body interactions of neutral bosons in optical lattices," P.R. Johnson, E. Tiesinga, J.V. Porto, C.J. Williams, New J. Phys., 11, 093022 (2009)