May 28, 2013
To describe the microscopic properties of matter and its interaction with the external world, quantum mechanics uses wave functions, whose structure and time dependence is governed by the Schrödinger equation.
In atoms, electronic wave functions describe - among other things - charge distributions existing on length-scales that are many orders of magnitude removed from our daily experience. In physics laboratories, experimental observations of charge distributions are usually precluded by the fact that the process of taking a measurement changes a wave function and selects one of its many possible realizations. For this reason, physicists usually know the shape of charge distributions through calculations that are shown in textbooks. That is to say, until now. In experiments that were recently performed at AMOLF, an international team of researchers led by Aneta Stodolna have succeeded in building a microscope that allows magnifying the wave function of excited electronic states of the hydrogen atom by a factor of more than twenty-thousand, leading to a situation where the nodal structure of these electronic states can be visualized on a two-dimensional detector. The results were published in Physical Review Letters and provide the realization of an idea proposed approximately three decades ago.
The development of quantum mechanics in the early part of the last century has had a profound influence on the way that scientists understand the world. Quantum mechanics extended the existing worldview based on classical, Newtonian mechanics by providing an alternative description of the micro-scale world, containing numerous elements that cannot be classically intuited, such as wave-particle duality, the importance of interference and entanglement, the Heisenberg uncertainty principle and the Pauli exclusion principle. Central to quantum mechanics is the concept of a wave function that satisfies the time-dependent Schrödinger equation. According to the Copenhagen interpretation, the wave function describes the probability of observing the outcome of measurements that are performed on a quantum mechanical system, such as measurements of the energy of the system or the position or momenta of its constituents. This allows reconciling the occurrence of non-classical phenomena on the micro-scale with manifestations and observations made on the macro-scale, which correspond to viewing one or more of countless realizations allowed for by the wave function.
Despite the overwhelming impact on modern electronics and photonics, grasping quantum mechanics and the many possibilities that it describes continues to be intellectually challenging, and has over the years motivated numerous experiments illustrating the intriguing predictions contained in the theory. For example, the 2012 Nobel Prize in Physics was awarded to Haroche and Wineland for their work on the measurement and control of individual quantum systems in quantum non-demolition experiments, paving the way to more accurate optical clocks and, potentially, the future realization of quantum computers. Using short laser pulses, experiments have been performed illustrating how coherent superpositions of quantum mechanical stationary states describe electrons that move on periodic orbits around nuclei. The wave function of each of these electronic stationary states is a standing wave, with a nodal pattern that reflects the quantum numbers of the state. The observation of such nodal patterns has included the use of scanning tunneling methods on surfaces and recent laser ionization experiments, where electrons were pulled out of and driven back towards their parent atoms and molecules by using an intense laser field, leading to the production of light in the extreme ultra-violet wavelength region that encoded the initial wave function of the atom or molecule at rest.
About thirty years ago, Russian theoreticians proposed an alternative experimental method for measuring properties of wave functions. They suggested that experiments ought to be performed studying laser ionization of atomic hydrogen in a static electric field. They predicted that projecting the electrons onto a two-dimensional detector placed perpendicularly to the static electric field would allow the experimental measurement of interference patterns directly reflecting the nodal structure of the electronic wave function. The fact that this is so, is due to the special status of hydrogen as nature´s only single-electron atom. Due to this circumstance, the hydrogen wave functions can be written as the product of two wave functions that describe how the wave function changes as a function of two, so-called “parabolic coordinates”, which are linear combinations of the distance of the electron from the H+ nucleus “r”, and the displacement of the electron along the electric field axis “z”. Importantly, the shape of the two parabolic wave functions is independent of the strength of the static electric field, and therefore stays the same as the electron travels (over a distance of about half a meter, in our experimental realization!!) from the place where the ionization takes place to the two-dimensional detector.
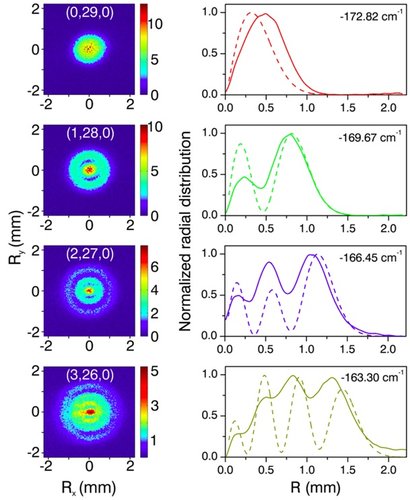
To turn this appealing idea into experimental reality was by no means simple. Since hydrogen atoms do not exist as a chemically stable species, they first had to be produced by laser dissociation of a suitable precursor molecule (hydrogen di-sulfide). Next, the hydrogen atoms had to be optically excited to the electronic states of interest, requiring another two, precisely tunable laser sources. Finally, once this optical excitation had launched the electrons, a delicate electrostatic lens was needed to magnify the physical dimensions of the wave function to millimeter-scale dimensions where they could be observed with the naked eye on a two-dimensional image intensifier and recorded with a camera system. The main result is shown in the figure below. This figure shows raw camera data for four measurements, where the hydrogen atoms were excited to states with 0, 1, 2 and 3 nodes in the wave function for the ? = r+z parabolic coordinate. As the experimentally measured projections on the two-dimensional detector show, the nodes can be easily recognized in the measurement. As this point, the experimental arrangement served as a microscope, allowing us to look deep inside the hydrogen atom, with a magnification of approximately a factor twenty-thousand.
Besides validating an idea that was theoretically proposed more than 30 years ago, our experiment provides a beautiful demonstration of the intricacies of quantum mechanics, as well as a fruitful playground for further research, where fundamental implications of quantum mechanics can be further explored, including for example situations where the hydrogen atoms are exposed at the same time to both electric and magnetic fields. The simplest atom in nature still has a lot of exciting physics to offer!
Reference A.S. Stodolna, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux, A. Gijsbertsen, J. H. Jungmann, C. Bordas and M.J.J. Vrakking
Hydrogen atoms under magnification: direct observation of the nodal structure of stark states
Phys. Rev. Lett. 110, 213001 (2013) | DOI: 10.1103/PhysRevLett.110.213001