1 May 2014
Twenty years ago, Philip Platzman and Allen Mills, Jr. at Bell Laboratories proposed that a gamma-ray laser could be made from a Bose-Einstein condensate (BEC) of positronium, the simplest atom made of both matter and antimatter (1). That was a year before a BEC of any kind of atom was available in any laboratory. Today, BECs have been made of 13 different elements, four of which are available in laboratories of the Joint Quantum Institute (JQI) (2), and JQI theorists have turned their attention to prospects for a positronium gamma-ray laser. In a study published this week in Physical Review A (3), they report detailed calculations of the dynamics of a positronium BEC. This work is the first to account for effects of collisions between different positronium species. These collisions put important constraints on gamma-ray laser operation.
The World’s Favorite Antimatter
Discovered in 1933, antimatter is a deep, pervasive feature of the world of elementary particles, and it has a growing number of applications. For example, about 2 million positron emission tomography (PET) medical imaging scans are performed in the USA each year. PET employs the antiparticle of the electron, the positron, that is emitted by radioactive elements which can be attached to biologically active molecules that target specific sites of the body. When a positron is emitted, it quickly binds to an electron in the surrounding medium, forming a positronium atom (denoted Ps). Within a microsecond, the Ps atom will spontaneously self-annihilate at a random time, turning all of its mass into pure energy as described by Einstein’s famous equation, E = mc2. This energy usually comes in the form of two gamma rays with energies of 511 kiloelectronvolts (keV), a highly penetrating form of radiation to which the human body is transparent. Platzman’s and Mills’ gamma-ray laser proposal involves generating coherent emission of these 511 keV photons by persuading a large number of Ps atoms to commit suicide at the same time, thus generating an intense gamma-ray pulse.
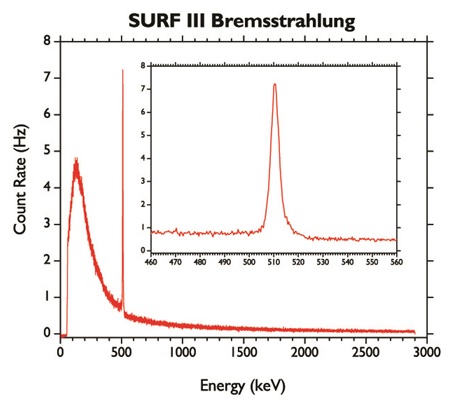
Figure 1: Spontaneous electron-positron annihilation observed at the SURF III Synchrotron Ultraviolet Radiation Facility at NIST. The main figure shows the intensity of detected radiation vs. energy in the gamma-ray region of the spectrum. The inset shows an enlargement of the sharp, intense feature at an energy of 511 keV, which is the energy equivalent of the mass of the electron according to Einstein’s formula E = mc2. Light at precisely that energy occurs when a high energy electron collides with a wall of the accelerator, creating an electron-positron pair. This positron later slows, enters into a Ps atom, and then annihilates to create gamma rays.
The Simplest Matter-Antimatter Atom
Ps lives less than a microsecond after it is formed, but that is a long enough for it to demonstrate the distinctive properties of an atom. It is bound by the electric attraction between positron and electron, just as the hydrogen atom is bound by the attraction between the proton and the electron. Figure 2 shows the spatial distribution of electron and positron density in Ps as given by the solution of the Schroedinger equation. The sharp central cusp is the place where the electron and positron meet, and annihilate. The electron density there is about four times the average density of the conduction electrons in copper wire.
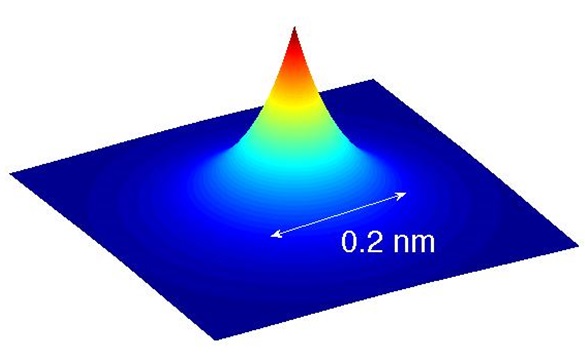
Figure 2.Solution of the Schroedinger equation for the electron-positron distance in Ps. Quantum mechanics tells us that the electron and positron are delocalized within Ps, with their distance described by a probability distribution. The central cusp is associated with zero relative distance, i.e. where the electron and positron are in the same place. This is where annihilation occurs. The electron density there is about four times the average density of the conduction electrons in copper wire.
Stimulated Annihilation
The electron and positron each has an intrinsic spin of ½ (in units of the reduced Planck constant). Thus, according to quantum mechanics, Ps can have a spin of 0 or 1. This turns out to be a critical element of the gamma-ray laser scheme. The 511 keV photons are only emitted by the spin-0 states of Ps, and this takes place within about 0.1 nanosecond after a spin-0 state is formed. The spin-1 states, on the other hand, last for about 0.1 microsecond, and only decay by emission of three gamma rays (for reasons of symmetry).
What we will get here is a process, stimulated annihilation, that is analogous to the stimulated radiation process at the heart of laser operation. Thus, when a pulsed beam of positrons is directed into a material, a random assortment of Ps states is created; the spin-0 states annihilate within the nanosecond, and the spin-1 states live for another nanosecond. During this latter time, the spin-1 states serve as an energy storage medium for the gamma ray laser: if they are switched into spin-0 states, which constitutes the active gain medium that generates the fast pulse of 511 keV gamma rays. Part of the JQI theorists’ work involves the modelling of the most likely switch for this process, a pulse of far-infrared radiation. They find several switching sequences that approach the optimal condition of switching all spin-1 states to spin-0 states in a time short compared to the annihilation lifetime.
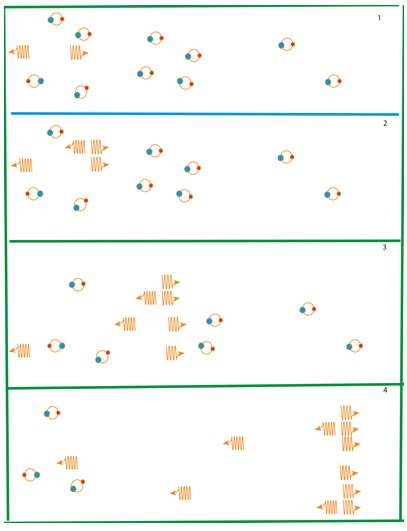
Figure 3. Schematic of the stimulated annihilation process in the positronium gamma-ray laser. Time sequence of frames, running top to bottom, suggests how some “seed photons” from spontaneous annihilation of a few Ps atoms will stimulate subsequent Ps annihilations, resulting in a pulse of 511 keV gamma rays
Positronium Sweetspot
Platzman and Mills pointed out that the Bose-Einstein condensate is a form of “enabling technology” for the Ps gamma-ray laser. This is because its low temperature and high phase-space density make coherent stimulated emission possible: in an ordinary thermal gas of Ps, the Doppler shifts of the atoms would suppress lasing action. This introduces another degree of complexity, which is explored in detail for the first time by the JQI team. A Ps BEC will only form when a threshold density of Ps is attained. That density depends upon the temperature of the Ps, but it is likely to be in the range of 1018 Ps atoms per cubic centimeter, which is about 3% of the density of ordinary air. At that density, collisions between Ps atoms occur frequently, and state-changing collisions are of particular concern. On the one hand, two spin-1 Ps atoms can collide to form two spin-0 atoms; this process limits the density of the energy storage medium. On the other hand, two spin-0 Ps atoms can collide to form two spin-1 atoms; this process limits the density of the active gain medium. Using first-principles quantum theory, the JQI team has explored the time evolution of a Ps BEC containing various mixtures of spin-0 and spin-1 Ps atoms, and has found that there is a critical density of Ps, above which collision processes quickly destroy the internal coherence of the gas.
The main conclusion of the JQI work is that the critical density is greater than the threshold density, so that there is a “sweet spot” for further development of a Ps gamma-ray laser. Dr. David B. Cassidy, a positronium experimentalist at University College London, who was not one of the authors of the new paper, summarizes it thusly:
“The idea to try and make a Ps BEC, and from this an annihilation laser, has been around for a long time, but nobody has really thought about the details of how a dense Ps BEC would actually behave, until now. This work neatly shows that the simple expectation that increasing the Ps density in a BEC would increase the amount of stimulated annihilation is wrong! Although we are some years away from trying to do this experimentally, when we do eventually get there the calculations in this paper will certainly help us to design a better experiment.”
(1) “Possibilities for Bose condensation of positronium”, P. M. Platzman and A.P. Mills, Jr., Physical Review B vol. 49, p. 454 (1994)
(2) The Joint Quantum Institute is operated jointly by the National Institute of Standards and Technology in Gaithersburg, MD and the University of Maryland in College Park.
(3) “Spinor Bose-Einstein Condensates of Positronium,”Yi-Hsieh Wang (汪以謝), Brandon M. Anderson (安博仁), and Charles W. Clark (查理斯克拉恪), Physical Review A, vol. 89, p. 043624 (2014) , published online 28 April 2014 at http://link.aps.org/doi/10.1103/PhysRevA.89.043624 DOI: 10.1103/PhysRevA.89.043624