01 June 2017
Researchers from ICFO and from the Univ of Naples report a flexible and efficient theoretical method which allows to measure the Zak phases of 1D systems and experimentally in a quantum walk of twisted photons.
Initially discovered in condensed matter, topological phases have so far been simulated in a variety of synthetic systems (ultracold atoms in optical lattices, photonic bandgap materials, mechanical systems, ...). Current theoretical research is showing that periodically‐driven systems, also called Floquet topological insulators, generate much richer and more complex topological properties than their static counterparts. Therefore, the accurate detection of these new topological properties in condensed matter and photonics is a key challenge.
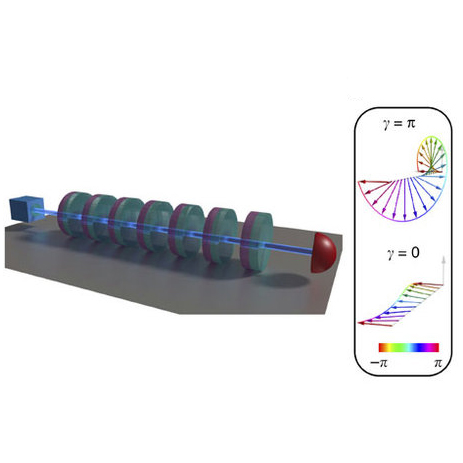
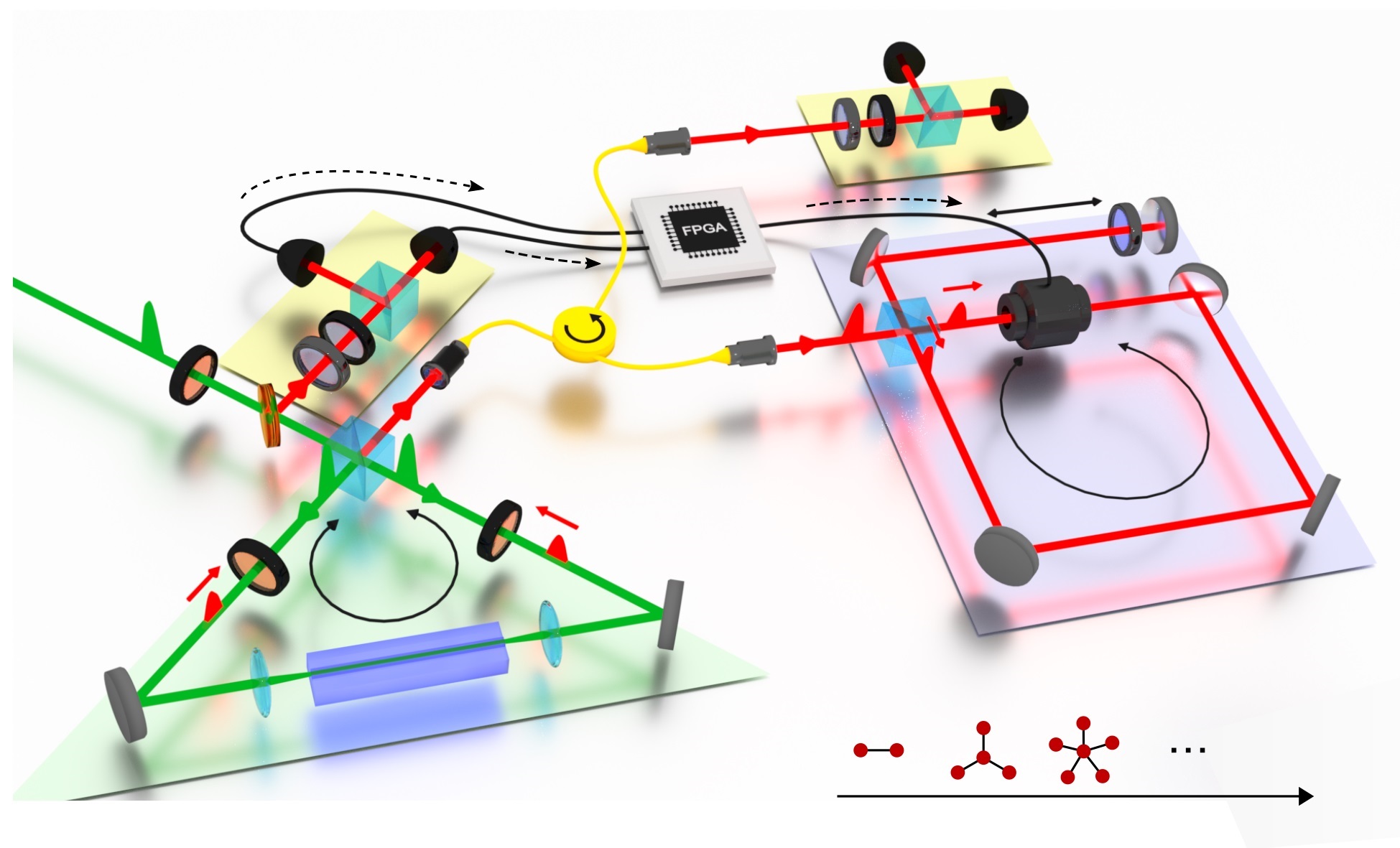
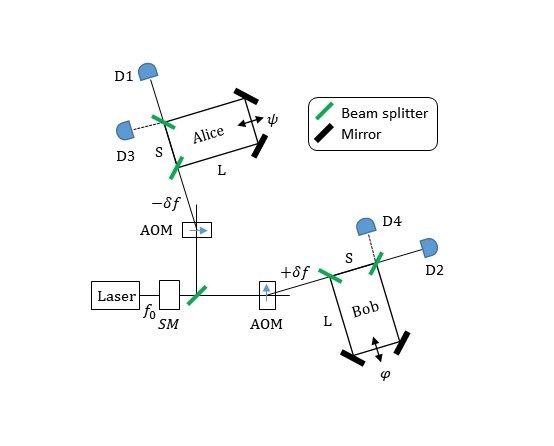
In the recent paper entitled "Detection of Zak phases and topological invariants in a chiral quantum walk of twisted photons", published in Nature Communications, ICFO researchers Alexandre Dauphin, Maria Maffei, Pietro Massignan, led by ICREA Prof at ICFO Maciej Lewenstein, in collaboration with the Filippo Cardano and coworkers at Federico II University of Naples, derive and design a flexible and efficient theoretical method which allows to measure the Zak phases of one dimensional systems with chiral symmetry by direct imaging of single particle dynamics in their bulk.
In their study, the researchers experimentally confirm their theoretical findings by measuring the two independent Zak phases of a chiral quantum walk realized by twisted photons, i.e., in a photonic platform exploiting the spin and orbital angular momenta of light. Combining the two phase windings, they provide a complete and robust topological characterization of this periodically‐driven system.
Finally, their method does not require a filled band, nor the application of a force, but simply relies on the observation of real‐time dynamics. This may be extremely beneficial in systems where uniform band filling is not easy to achieve, such as the ones not affected by the Pauli principle (e.g., bosonic atoms, phonons, and photons).